To address the frequency-selective channel fading and hardware implementation constraints of broadband multiantenna millimetre-wave systems, a hybrid digital-mode beamforming algorithm combining single-carrier frequency-domain equalisation technology is proposed. The coefficients of the beamforming matrix and the equaliser are optimised based on the minimum mean square error of the equaliser output signal. In order to reduce the solution complexity, an iterative antenna array training technique is applied to decompose the original optimisation problem into local optimisation problems at the base station and the subscriber end, so that the coefficients that need to be optimised can be converged by the alternating iterative algorithmic processing at both ends of the communication. Simulations show that the proposed new algorithm has a performance gain of about 2 dB in signal-to-noise ratio over the conventional algorithm at an error rate of 10-4 .
In terms of the development of wireless mobile communication, the 1st and 2nd generations (1G and 2G) have addressed the voice communication needs of people in both analogue and digital ways, respectively; the 3rd generation (3G) has added the support for data services; the 4th generation (4G) has focused on meeting the growing needs of people for data services; and the future 5th generation (5G) will continue to support the needs of user data services with higher transmission rates, but will also be able to meet the needs for data services at higher rates. In the future, the 5th generation (5G) mobile communication system will not only continue to support higher transmission rates for user data services, but will also need to support the access and connection of a large number of smart devices to support new and diversified services such as smart grids, smart homes, smart cities, virtual reality, remote education and remote healthcare, in tandem with the rapid development of the Internet of Things (IoT). It is expected that by 2020, more than 50 billion smart devices will be connected to wireless networks, and the data capacity of wireless networks will be 1,000 times that of today. In order to meet the 1,000-fold increase in capacity by 2020, three dimensions of the problem have been recognised: the adoption of higher communication bands for greater bandwidth, increased spectrum utilisation, and frequency multiplexing through the demarcation of high-density communities.
Broadband millimetre wave communication is very closely integrated with these three dimensions: firstly, the millimetre wave band is defined in the range of 30-300 GHz, which can provide hundreds of megahertz or even gigahertz of communication bandwidth, and it is the most direct way to solve the problem of capacity; secondly, from the perspective of increasing spectrum utilisation, large-scale antennae are widely recognised as an effective technology, and the existing communication bands are not as effective as the existing ones due to the wavelengths in the sub-metre or centimetre range. The existing communication frequency bands, with their wavelengths at the decimetre or centimetre level, are limited in size and volume, making it difficult to form large-scale antenna arrays, while the natural content of millimetre wave determines its effectiveness in combining with large-scale antenna; and lastly, the traditionally perceived weaknesses of millimetre-wave communications in terms of high path loss and short transmission distance due to high frequency have become the very strengths of frequency multiplexing in high-density communities.
Currently, most of the commercially available millimetre wave communication standards and systems are limited to indoor communications in the 60 GHz free band, such as the IEEE 802.15.3c [7] and 802.11ad standards [8]. With the development of microelectronics technology and the increasing demand for mobile communication services, millimetre-wave communication has become one of the most important candidates for outdoor wireless mobile communication applications within a 200 m radius area.
However, the propagation characteristics of millimetre-wave signals bring new problems and challenges for system design. Under the condition of the same antenna gain, millimetre-wave has a large path loss and poor transmission and bypass capability compared with microwave frequency bands below 6 GHz [3-6]. In order to cope with this problem, millimetre wave systems usually need to put down dozens or even hundreds of antennas at the transceiver end to form an array to obtain a high directional gain to compensate for the energy loss in transmission. As a result, a multi-antenna design with self-adjusting beamforming (BF) is the first and foremost necessary technology to ensure millimetre-wave micro-area coverage.
Compared with the existing mobile communication systems in the frequency bands below 6 GHz,broadband millimetre-wave systems have three differences and challenges in BF design: firstly, the implementation pipeline of the system's multi-antenna transmission is limited by the hardware cost and power overhead. Compared with existing mobile communication systems, the hundreds of megahertz or even gigahertz communication bandwidth of mmWave systems significantly increases the hardware cost and power consumption. In the case of an analogue-to-digital converter (A/D), for example, an A/D based on the latest complementary metal oxide semiconductor (CMOS) process with 12 bits precision, 100 Ms/s sampling rate, and support for a 16-channel antenna consumes more than 250 mW of power [5]. Under these constraints, it is not possible to put a set of radio-frequency (RF) connections for each antenna, and therefore, it is difficult to adopt an all-digital implementation scheme for practical millimetre-wave multi-antenna technology.
Secondly, the antenna array size in mm-wave systems is very large, with the number of antennas reaching dozens or even hundreds. The use of large-scale antennas has increased the freedom of system design, but it has also made the problem of BF matrix optimisation more complex. Finally, compared with the mobile communication systems in the frequency bands below 6 GHz, the millimetre-wave channel is sparse in both delay and angle domains, which provides an effective way to reduce the complexity of the BF design, but at the same time, it also brings a new challenge to the problem solving [9]. Based on the above three points, researchers have proposed a hybrid BF (HBF) pipeline based on mixed digital-analogue signal processing by combining analogue and digital circuits. HBF has also gradually attracted extensive attention from both academia and industry, and has gradually become a key technology for millimetre wave communications.
1.Current state of millimetre wave HBF research
The following figure illustrates the HBF of a single user with multiple data flow transmissions using the millimetre wave downlink from the base station to the user as an example.
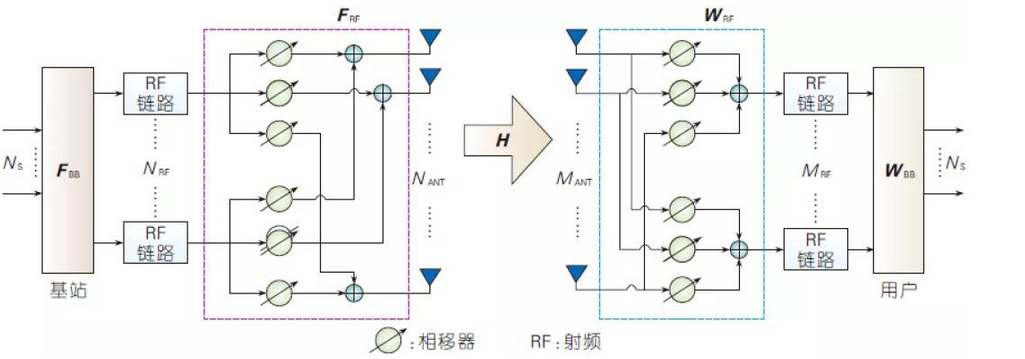
Millimetre-wave digital-mode hybrid beamforming schematic
In the above figure, the matrices FBB and FRF marked in red are the base station-side digital and analog BF matrices respectively, and the matrices WBB and WRF marked in blue are the user-side digital and analog BF matrices respectively.
Compared with the all-digital BF structure usually adopted in existing wireless communication systems in the frequency band below 6 GHz, the HBF in millimeter-wave systems has the following differences and difficulties: with the increase of the number of antennas, the size of the HBF matrices increases, and the optimisation difficulty and computational complexity are added; the optimisation of the HBF, especially for the processing of analog signals, needs to take into account the implementation pipeline of the analog circuits and the characteristics of the analog devices, such as phase shifter The structure of the HBF brings new challenges in channel estimation, since the channels that can be estimated in the digital domain are cascades of the actual air-port channel and the analogue BF matrix.
The double sparsity of millimetre wave transmission in the delay and angular domains also brings new challenges to channel estimation and HBF matrix solving. In broadband systems, unlike digital BFs, analog BFs are consistent for all subcarriers in the bandwidth (or all frequency components of the corresponding signals in case of single-carrier communications) because they process the analog signal after the digital-to-analogue converter (D/A) and before the A/D.
Existing HBF design studies have focused on narrowband fading models and have been optimised with systematic mutual information, i.e:
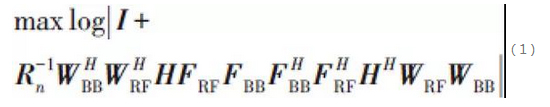
where the received signal power is normalised and Rn is defined as the noise covariance matrix after HBF processing at the receiver. As shown in Fig. 1, when the analog BF is composed of a phase shifter and an adder, each element of the matrices FRF and WRF has a modulo 1 constraint (only the phase parameter can be optimised). There are two ways of analogous BFs, i.e., fully connected and partially connected, which is reflected in the fact that each element of the matrices FRF and WRF needs to be optimised in the former pipeline, while in the latter pipeline it is presented in the form of block diagonal matrices. Currently there are two mainstream solutions to the problem in Eq. (1), fixing the WBB and WRF first and then optimising the FBB and FRF, specifically:
Using the angular domain sparsity property of the millimeter-wave channel, the problem of solving the FBB and FRF is transformed into a sparse approximation problem and solved by using the orthogonal matched pursuit (OMP) algorithm, whose limitation lies in the fact that the range of values of the column vectors in the FRF corresponds to the labels of the spatial beam angles, and the degrees of freedom of the antique products are restricted. In addition, this algorithm requires complete channel information in the solution process.
In large-scale MIMO systems, the assumption that the columns of the FRF are orthogonal to each other can be adopted, so that the joint optimisation of the FBB and the FRF can be folded into a step-by-step optimisation of both. Compared with the first algorithm, this algorithm does not depend on the sparsity of the channel and does not require labelling of the column vectors in the FRF; however, this algorithm is based on the assumption of large-scale antennas, and its performance depends on the correlation between the number of antennas, the number of RF links, and the number of baseband data flows. This algorithm also requires complete channel information.
Based on the narrowband HBF, the researchers propose a broadband HBF algorithm combined with orthogonal frequency division multiplexing (OFDM) to combat frequency selective fading in broadband millimetre-wave channels, and the optimisation objective is extended to maximise the rate sum over multiple subcarriers.
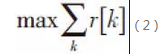
included among these
![]()
Note that unlike the digital BF matrices FBB[k] and WBB[k] which are related to the subcarrier index number k, the values of the analogue BF matrices FRF and WRF are independent of the subcarrier index number k. The HBF matrices FRF and WRF are not related to the subcarrier index number k, but they are related to the subcarrier index number. The existing solution to the problem in Eq. (2) continues the design idea of HBF under narrowband fading, but whether the assumption that the analogous BF matrices are restricted to be in the form of labels under narrowband, or have an approximate orthogonal nature [11] is appropriate, or whether it is approximate optimal, in broadband communication scenarios is yet to be further proved. In addition, existing broadband algorithms still require full channel state information, which will further reduce the usefulness of the algorithms.
2.HBF in Single Carrier Broadband Millimetre Wave Systems
Single Carrier Frequency Domain Equalisation (SC-FDE) and OFDM are nowadays recognised as the main technologies that can effectively combat channel frequency selective fading [16-17]. SC-FDE has been adopted as an uplink transmission scheme by the 3rd Generation Partnership Project (3GPP) Long Term Evolution (LTE)/Enhanced LTE (LTE-A) standard due to the lower peak-to-average power of the transmitted signal using a single-carrier transmission pipeline. (LTE-A) standard.
In broadband millimetre-wave communication systems, the A/D accuracy must be sacrificed in order to support hundreds of megahertz or even several gigahertz of communication bandwidth from the considerations of realisation cost and device power consumption. Single-carrier modulation has a relatively small dynamic range of the signal compared to multi-carrier modulation, which reduces the requirement of the A/D quantisation accuracy. The following figure shows the BER performance comparison between single-carrier and multi-carrier (OFDM, for example) under different A/D quantisation accuracies with four-phase phase-shift keying (QPSK) and 16-symbol quadrature amplitude modulation (QAM) in Gaussian channel, and it can be seen that: OFDM has higher requirements on A/D quantisation accuracies. From this point of view, single carrier can well balance the performance and hardware to achieve the complexity requirements, which makes it one of the most important candidates for millimetre wave micro-area.
Currently, there are few studies on the HBF algorithm for wideband millimeter-wave combined with SC-FDE. In this paper, we will take the example of a single RF link scenario with a single data flow to illustrate the modelling and solving of the HBF optimization problem for a single-carrier wideband millimeter-wave system.
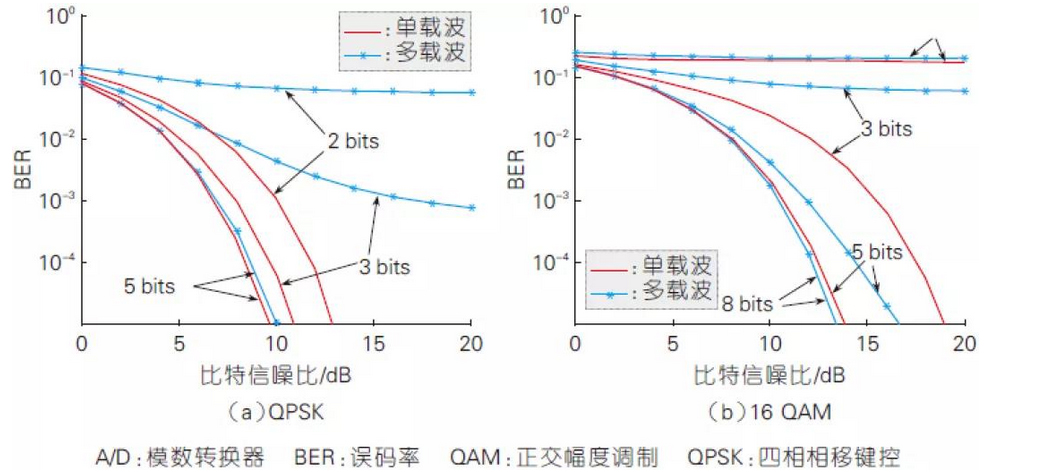
Performance Comparison of Single-Carrier and Multi-Carrier Systems with Finite A/D Accuracy (Gaussian Channel)
2.1 System Modelling
In the single RF link scenario, the HBF optimisation problem in Fig. 1 degenerates into the optimisation problem with analogous BF vectors in Fig. 3. The difference is that after the analog BF at the base station and at the user, the original air-port Multiple-Input Multiple-Output (MIMO) frequency-selective fading channel is degraded to a Single-Input Single-Output (SISO) frequency-selective fading channel in the baseband, which needs to undergo the Frequency Domain Equalisation (FDE) process. To address this feature, we propose a hybrid digital-analog signal processing that combines analog BF and digital FDE, and at the same time jointly optimise the coefficients of analog BF and digital FDE based on the criterion of minimising the mean-square error (MSE) of the FDE output signals.
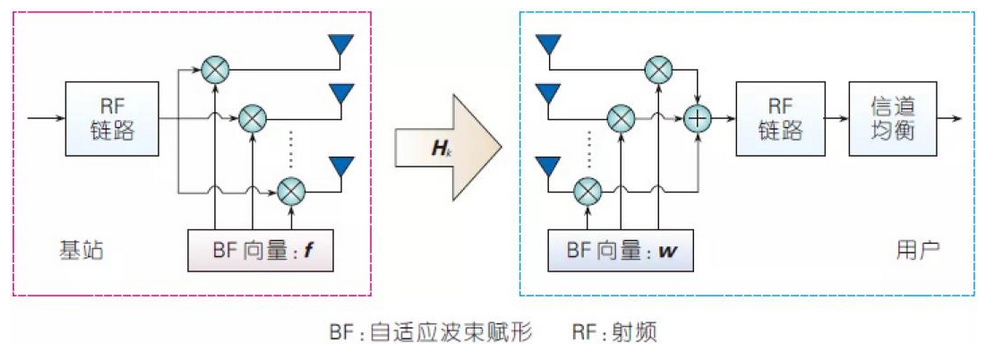
Millimetre-wave analogue beamforming in a single carrier wave transmission pipeline.
Define the BF vectors of the base station and the user as f and w, respectively, then the frequency response of the equivalent SISO channel in the baseband is wHHkf, where Hk is the response matrix of the channel at the kth frequency component. Taking the linear FDE as an example, the optimal FDE coefficients using the minimum mean square error (MMSE) criterion can be obtained along with the corresponding MSEs, which are obviously functions of f and w. It can be shown that based on the MMSE criterion, the frequency response of the baseband equivalent SISO channel is wHHkf. It can be shown that the single carrier HBF optimisation problem based on the MMSE criterion can be modelled as:
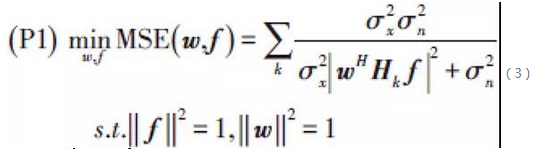
included among these
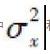
![]()
signal and noise power, respectively. The optimisation problem (P1) is a non-convex problem, which is difficult to obtain an optimal solution, and a direct solution also requires knowledge of the full channel information Hk. A possible optimisation method is for the user to first estimate the channel matrix, and then to obtain a suboptimal solution for f and w based on a certain arithmetic law, and then echo the result of f back to the base station. However, this method is not suitable for millimetre wave systems because the large antenna pattern adds complexity to the channel estimation. In addition, since there is not enough antenna and spatial diversity gain in the channel estimation, the user's received signal-to-noise ratio (SNR) is very low, and in order to guarantee the quality of the channel estimation, longer training sequences need to be used, which adds to the training time and training overhead.
To address this problem, we adopt the Iterative Antenna Array Training (IAT) technique, as shown in Fig. 4, to take advantage of the reciprocity between the uplink and downlink channels in Time Division Duplex (TDD) mode by fixing the BF vectors at one end of the communication link and optimising the BF vectors at the other end, so that the original problem is folded into a local sub-optimisation problem at the two ends of the BS and the subscriber, and then optimise the problem by alternating the IAT, so that the BF vectors at both ends can eventually converge to the full domain or the subscriber's BF vector. The BF vectors at both ends are then optimised by alternating iterative operations, so that the BF vectors at both ends can be converged to the global or local optimal solution. The advantage of the IAT method is that the complexity of the channel estimation can be reduced from O(NtNrL) to O(NtL + NrL), where Nt, Nr represent the number of antennas at the base station and at the subscriber, respectively, and L represents the length of the multipath channel.
Although the IAT-based BF algorithm is very attractive in reducing the complexity of channel estimation, there are still considerable difficulties and challenges in the design of the specific algorithm, e.g., what optimisation targets should be chosen? Can the original optimisation problem be folded into two sub-optimisation problems? Whether the astringency can be proved, etc. We have shown that the problem (P1) can be folded into two local sub-optimisation problems at the base station and the subscriber end using the IAT pipeline, and can eventually converge to a suboptimal solution of the original problem [19]. Before describing the detailed solution steps, we first review in Section 2.2 a traditional iterative eigenvalue decomposition algorithm based on IAT technology with the total channel power as the optimisation objective.
2.2 Traditional algorithm
In millimetre-wave systems deploying a single RF link, the literature [13], [20] proposes a single-carrier wideband analogous BF algorithm with the optimisation objective of maximising the total power of the equivalent SISO multipath channel. The optimisation problem can be modelled as:
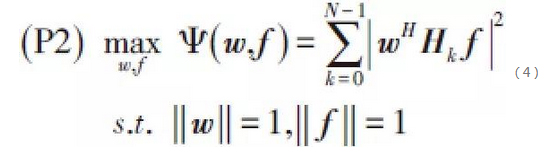
In order to solve the optimisation problem (P2), based on the IAT technology, the original problem is degenerated into the following sub-optimisation problem at the client side, given the transmit BF vector f at the base station:
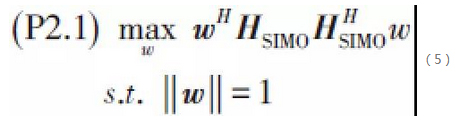
The eigenvector corresponding to the maximum eigenvalue of the matrix. Where HSIMO = [hSIMO, 0...hSIMO, N -1], hSIMO, k = Hkf is the equivalent single-input multiple-output (SIMO) channel from the RF link inlet of the base station to the subscriber antenna array. It can be shown that the optimal solution of the optimisation problem is
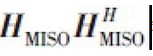
Similarly, when given the user's transmit BF vector w, the sub-optimisation problem that exists at the base station side is:
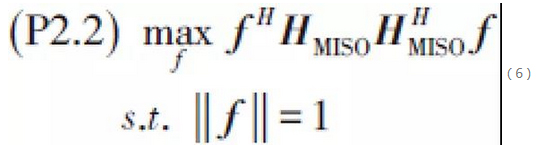
where HSIMO = [hSIMO, 0...hSIMO, N -1],![]() is the equivalent multiple-input single-output (MISO) channel from the base station antenna array to the user RF link exit. The sub-optimisation problem with has the same form. The optimal f is
is the equivalent multiple-input single-output (MISO) channel from the base station antenna array to the user RF link exit. The sub-optimisation problem with has the same form. The optimal f is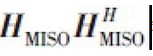
The eigenvector corresponding to the maximum eigenvalue of the matrix.
The above BF design aims at maximising the total channel power without considering the effect of selective fading of the equivalent SISO channel frequency. Compared with this conventional algorithm, our proposed design criterion aiming at minimising the MSE of the output signals of the equaliser can better meet the final transmission performance target of the system.
2.3 New algorithm
In Section 2.1, we propose a new algorithm that combines the analogous BF with the digital FDE for joint optimisation, and is based on the criterion of minimising the MSE of the FDE output signal. Combining the IAT principle (shown in Fig. 4), we decompose the original problem as follows: when the BF vector f is fixed at the base station, the optimisation problem degenerates into a sub-optimisation problem of w at the client side. Specifically as Eq:
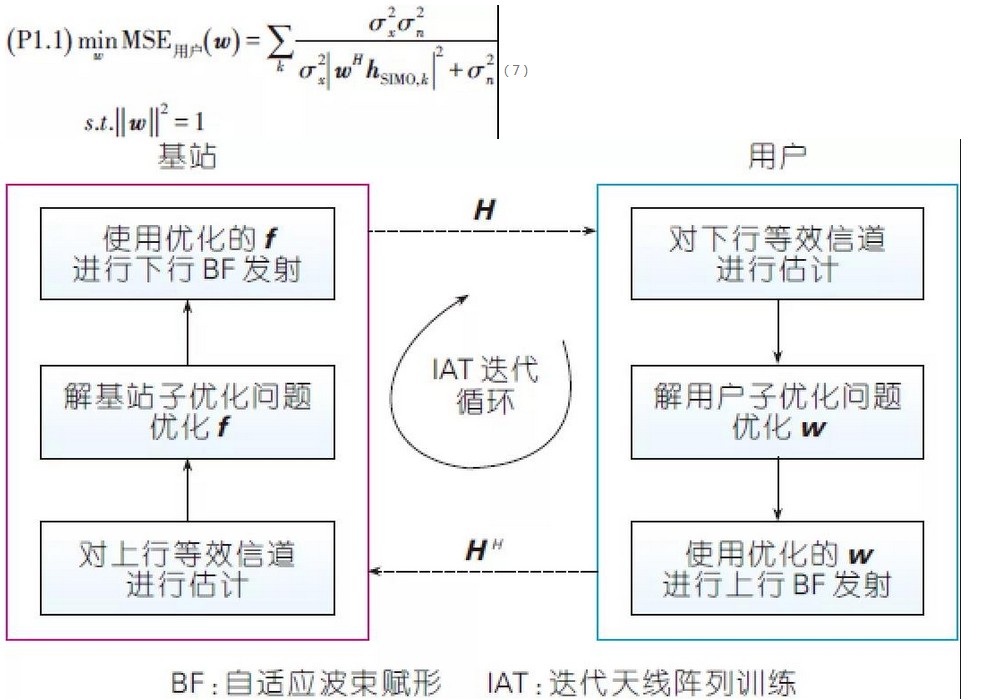
IAT-based Iterative Computing Optimisation Schematic
Similarly, when the user fixes w as the transmitting BF vector in the uplink, the optimisation problem (P1) can again be degraded to a sub-optimisation problem of f at the base station end, i.e., based on the reciprocity of the TDD uplink and downlink channels:
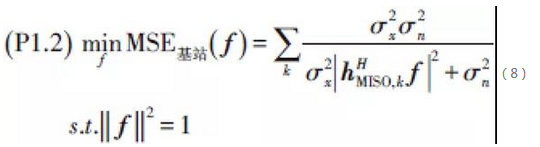
We show that by back-and-forth iterative algorithmic optimisation between (P1.1) and (P1.2), it is eventually possible to converge f and w to a locally optimal solution of the original problem (P1). The optimised problems (P1.1) and (P1.2) are still non-convex and it is difficult to obtain a global optimal solution. We can use the classical gradient descent algorithm to obtain a local optimal solution to the problem.
Since (P1.1) and (P1.2) are non-convex problems, whether the gradient descent algorithm can yield a better local optimal solution depends on the selection of the initial vector. The initial point of the local optimisation problem can be obtained by solving an approximation (or upper and lower bound) of the original problem. It can be found that the objective function in the problem (P1) can be regarded as the inverse of the summed mean of several sub-projects, and according to the Cauchy's inequality, they are greater than or equal to the inverse of their arithmetic mean, and the optimisation of this arithmetic mean is consistent with the objective function of (P2), and therefore an efficient way of selecting the initial values of (P1.1), (P1.2) is to use a solution of the problem (P2).
2.4 Simulation results
The MIMO channel on the kth frequency component can be modelled as:
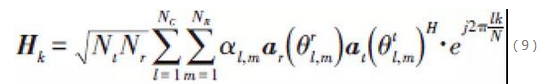
where NC and NR denote the number of clusters of paths in the channel and the number of paths in each cluster, respectively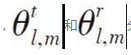
denote the angle of horizontal emission (AOD) and the angle of horizontal arrival (AOA) of the mth path in the lth cluster, respectively, and α l, m denote the transmission complex gain of the mth path in the lth cluster,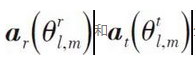
The antenna response vectors of the base station and the subscriber are represented respectively [14-15]. In the simulation, the BTS and the subscriber are each equipped with a linear antenna array consisting of 16 antennas spaced by half wavelength, and each data block contains 64 QPSK symbols.
Fig. 5 shows the BER performance curves of the conventional algorithm aiming at maximising the total channel power and the new algorithm aiming at MMSE at different SNRs. For fairness, the total number of IAT iterations is set to 6 for both algorithms. In the new algorithm, according to the elaboration in Section 2.3, the result after two iterations of the conventional algorithm is used as the initial vector of the new algorithm in the simulation, so the first two IAT treatments of the new algorithm are the same as that of the conventional algorithm. From Fig. 5, it can be seen that the new algorithm is able to obtain better spatial diversity gain than the traditional algorithm. For example, the new algorithm has about 2 dB SNR gain over the conventional algorithm at BER=10-4 . In addition, we also consider the phase shifter with finite quantisation bits for BF implementation in the actual system, which operates on the basis of the original algorithm by retaining only the phase portion of each element of the BF vector in each iterative operation and setting the mode fixation to a constant. Fig. 5 shows the BER performance when the phase quantisation accuracy is Q=4 bits. It can be seen that both algorithms have some performance loss due to the implementation pipeline of the finite-precision phase shifter, but the new algorithm still has significant performance gain over the traditional algorithm.
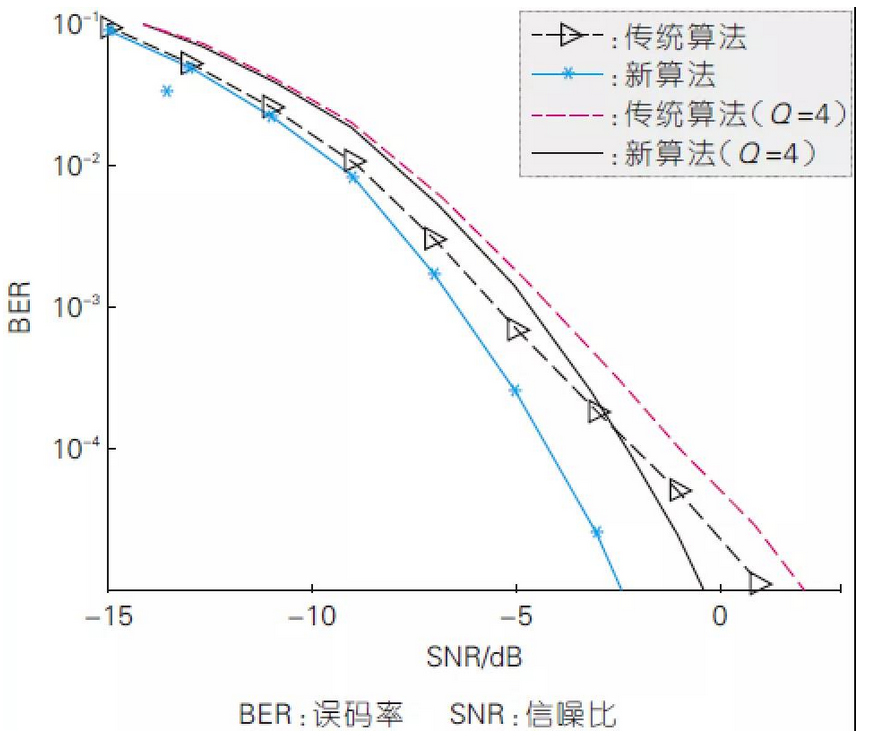
Error bit rate performance of new and conventional algorithms at different signal-to-noise ratios
Fig. 6 compares the BER performance of the new algorithm with that of the traditional algorithm under different iterative operations, where the SNR is fixed at -4 dB. It can be seen from the figure that, because the new algorithm adopts the traditional algorithm's two iterative operations to obtain the initial vectors, the two algorithms have the same performance for the first two iterative operations, but the traditional algorithm's performance gain is very limited from the 3rd time onwards, while the new algorithm's performance in the 3rd iteration is about one order of magnitude higher due to the targeting of MMSE, and converges rapidly in the subsequent iterations. However, from the 3rd iteration onwards, the performance gain of the traditional algorithm is very limited, while the performance gain of the new algorithm is very limited in the 3rd iteration due to the targeting of the MMSE, the BER performance is rapidly increased by one order of magnitude, and then rapidly converged in the subsequent iterations.
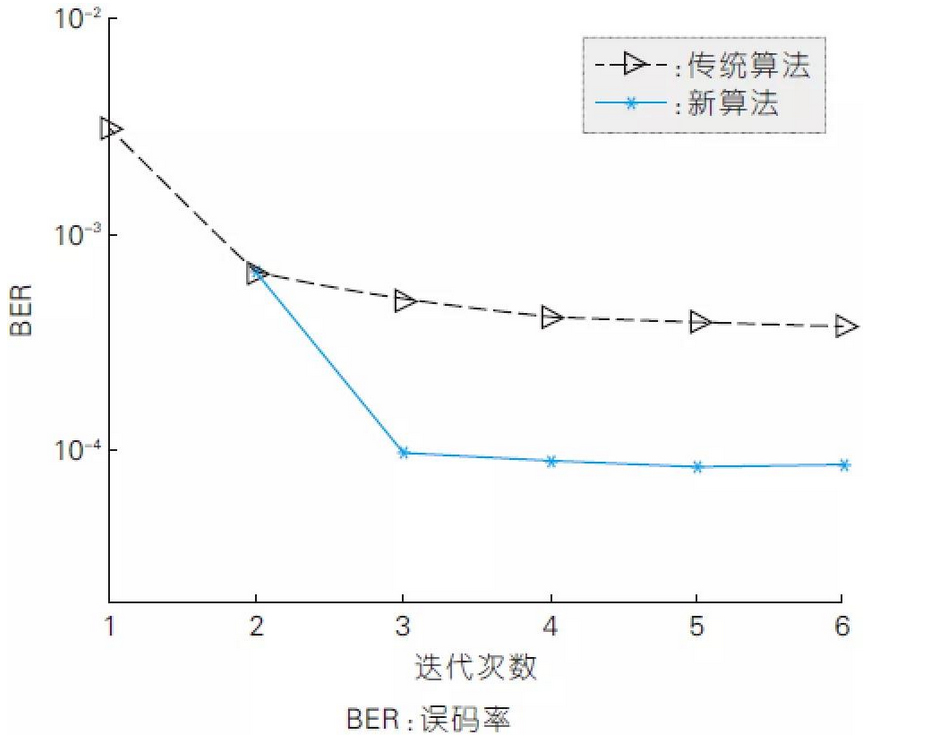
Error Bit Rate Performance of the New Algorithm and the Existing Algorithm with Different Iteration Times
3.Conclusion
Millimeter-wave communication is a key technology that can guarantee a great capacity increase for 5G and even the future newer generation of wireless mobile communication systems, and HBF technology is an important research issue to ensure that millimeter-wave systems can take advantage of their large-scale antenna arrays to overcome the effects of transmission power loss and channel fading while taking into account both the cost of hardware realisation and power consumption. In this paper, based on the review of existing millimeter-wave HBF research progress, we propose the design idea of joint optimisation of SC-FDE and HBF for millimeter-wave channels with frequency-selective fading and system hardware constraints on RF linking, and establish the millimeter-wave HBF optimisation problem under a single-carrier transmission pipeline based on the criterion of minimising the MSE of the channel equilibrium. In solving the problem, considering the complexity of estimation carried out by large-scale multipath MIMO channels, we apply the IAT method to decompose the original problem into two local sub-optimisation problems at both the base station and user ends, and take advantage of the reciprocity between the TDD uplink and downlink channels, and the pipeline processed by alternating and iterative operations can ensure that the local optimal solutions can be converged at both ends. Numerical simulation results show that the new algorithm can have more than 2 dB performance gain in SNR over the traditional algorithm.
In our future work, we will extend the system model of single RF link and single data flow mentioned in the paper to the scenario of multiple RF links and multiple data flows, and design the HBF algorithm for this scenario using the IAT method. We will also consider exploiting the double sparsity of the millimetre wave channel in the delay and angle domains in the multi-user scenario, using the multi-user MSE as an optimised performance metric, and incorporating IAT techniques to design efficient broadband millimetre wave digital-mode hybrid multi-user access algorithms to enhance the system's multi-user spatial access capability. In addition, most of the existing HBF studies assume ideal channel estimation, accurate A/D conversion, and high-precision phase shifters, but in reality, the non-ideal nature of these parameters or devices will have an impact on the system performance, and the study of robust HBF design is also of great significance and application value. Finally, the IAT-based HBF algorithm relies on the reciprocity of the uplink and downlink channels in TDD mode, and the inconsistency of the characteristics of the uplink and downlink devices exists in the actual system, so how to carry out more effective channel calibration is also an important issue worth studying.